Wednesday, November 8th, 2017...4:30 pm
“Cipher? I Don’t Even Know Her:” The History of Zero and its Philosophical Implications
Emily Huel
https://giphy.com/gifs/the-to-do-list-eszoVAyBO2X8Q
GIF: GIPHY.
Introduction:
From the Old English form nan þinc, the word nothing, as defined by the Oxford English Dictionary, is “no part, share, or quantity of a thing; no aspect, evidence, or quality of a thing or person” (OED s.v. nothing, n. sense 2a). The first written evidence of the word was in the Vitas Patrum, which was written in Old English: “þa ne gefredde he ne naþinc þæs brynes for þam miclan luste” (OED s.v. nothing, n sense 2a). Since first written records in English were composed during this time (Liu A.45), it is safe to assume that nothing pre-existed the Vitas Patrum. While the terms zero and nothing are used within similar contexts by native English speakers, the two terms originally had different meanings and origins. However, the mathematical function of a third word – cipher, or <0> – has subtly changed the definitions of both words in such a way that transforms the absence of existence into an object in its own right.
Zero:
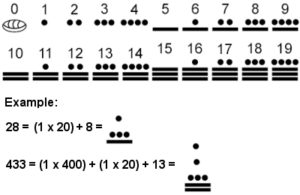
Mayan number System. Image: Story of Mathematics.
The concept of zero is believed to be thousands of years old. The Mayans, who lived in what is now known as Mexico, were familiar with the notion of “nothingness.” Across the Atlantic Ocean, Claudius Ptolemy, inspired by the Babylonians, began to use a symbol contextually similar to the modern zero as a place-holder, and in seventh-century India, Brahmagupta expanded the idea and created a set of rules for the place-holding zero (Crilly 4).
While the English word zero was loaned from the French language during the seventeenth century (OED s.v. zero, n. sense 1a), the mathematical figure came from the Old French word cyfre, which itself came from the Arabic word çifre:
An arithmetical symbol or character (0) of no value by itself, but which increases or decreases the value of other figures according to its position. When placed after any figure or series of figures in a whole number it increases the value of that figure or series tenfold.
According to the Oxford English Dictionary, the first written evidence of cipher as a mathematical place holder occurred in 1399 in the poem Richard Redeles: “Than satte summe, as siphre doth in awgrym, That noteth a place, and no thing availith” (OED s.v. cipher, n. sense 1a).
However, if one compares the definition of nothing to the definition of cipher, it becomes apparent that cipher and nothing do not mean the same thing. Thus, while cipher does technically mean “nothing,” the definition implies that “nothing” has the ability to affect its surroundings. Therefore, the mathematical connotation that accompanies cipher or zero adjusts the concept of “nothing” and objectifies it, thereby turning a nothing into a something.
Zero and Metaphysics:
However, some philosophers argue that it is possible for a “nothing” to exist in the same way that an object exists. When one asserts the existence of something, then it us up to them to provide evidence (Sorenson n.p.), and if the Oxford English Dictionary is defined as an absence of evidence (OED s.v. nothing, n. sense 2a), then it is impossible to assert the existence of nothing and objectify it. Nonetheless, English speakers objectify – albeit subconsciously – nothing on a regular basis. Consider this example: are there really holes in Swiss cheese? A native English speaker, when describing a slice of Swiss cheese, would usually say “there are holes in this cheese,” rather than “there is no cheese within these holes” (Sorenson n.p.). This is where English speakers’ usage of nothing is influenced by the mathematical concept of zero, or rather cipher. Zero – or rather <0> – is used as a placeholder. For example, without <0>, one would never be able to tell the difference between 75 and 705 (Crilly 4). Thus, it can be argued that in the Swiss cheese is used as a placeholder within the entire “sum” of the cheese, and while the holes do not increase the value of the surrounding cheese, like a <0> would in a numerical figure, it can be argued that English speakers, subconsciously, believe that the holes in the cheese are “objects” that have a particular influence on their surroundings.
Yet, should mathematical concepts be considered part of the English language? To some, zero, or rather <0>, is simply a figure that exists outside of natural language (Rotman 87). English speakers often use other mathematical terms in a non-mathematical context (for example, “I would like to add my opinion to the debate”). However, should we consider the symbol <+> and the word add to be synonymous? Should mathematical symbols be considered ideograms in the same vein as emojis, or should mathmatical notation be considered its own “quasi-language” that is utilized through the process of code-switching? Nevertheless, as numbers, like words, are socially-constructed “representations” of concepts, then it stands that mathematical figures – and their associated words – would function in a way similar to any other word.
Conclusion:
While zero and nothing came from differing backgrounds, zero – or rather cipher and <0> – added an additional nuance to the meaning of nothing that allows the concept to be treated as an object. While it is unclear whether or not mathematics is definitively a part of the English language, the descriptive use of the word nothing seems to imply that the subject affects the way that we use languages at a potentially metaphysical level.
Works Cited:
Crilly, Tony. 50 Mathematical ideas you really need to know. London: Quercus, 2007. Print.
Liu, Yin. “Describing the History of English.” ENG 290.6 (01) Introduction to English Linguistics and History of English Language. Fall/Winter 2017/2018. University of Saskatchewan Bookstore. A.43-A.46. Print.
[OED] Oxford English Dictionary Online. Oxford UP, June 2017, http://www.oed.com/view/Entry/33155?rskey=cqkYVV&result=1#eid. Accessed 25 October 2017.Rotman, Brian. Signifying Nothing: The Semiotics of Zero. Basingstoke: Macmillan P, 1987. Print.
Sorensen, Roy. “Nothingness.” The Stanford Encyclopedia of Philosophy. Edited by Edward N. Zalta. Fall 2017 ed. The Metaphysics Research Lab, 2017. https://plato.stanford.edu/entries/nothingness/#TheMosOneEmpWor. Accessed 25 October 2017.
Comments are closed.