By Rina Rast for ASTR 310

This post aspires to present a description of how the first galaxies formed in the early universe. Since this topic is broad enough to warrant an entire textbook all to itself, this post will focus on key information and theory. The discussion requires some basic knowledge about specific stages of the Big Bang and the formation of the Cosmic Microwave Background radiation, which will be the focus of the first section of this summary. From there, we will discuss density perturbations in the expanding, cooling universe. This will give enough background information to tackle the main target: how matter in the universe clumped into galaxies.

Big Bang, In Brief

The current standard model for the universe is referred to as the “Hot Big Bang” model. In this model, the universe began expanding from a very hot, dense state in an instant that was a finite time in the past. All of modern physics currently points toward this model of the universe. Fundamental observations supporting this theory include the relation of redshift to distance (leading to the conclusion that the universe is expanding), the observed isotropy and homogeniety of the universe, as well as the existence of the Cosmic Microwave Background radiation. However, the aim of this discussion is to cover details of the Big Bang rather than to examine the various lines of evidence for it, so the reader is encouraged to investigate these topics on their own.

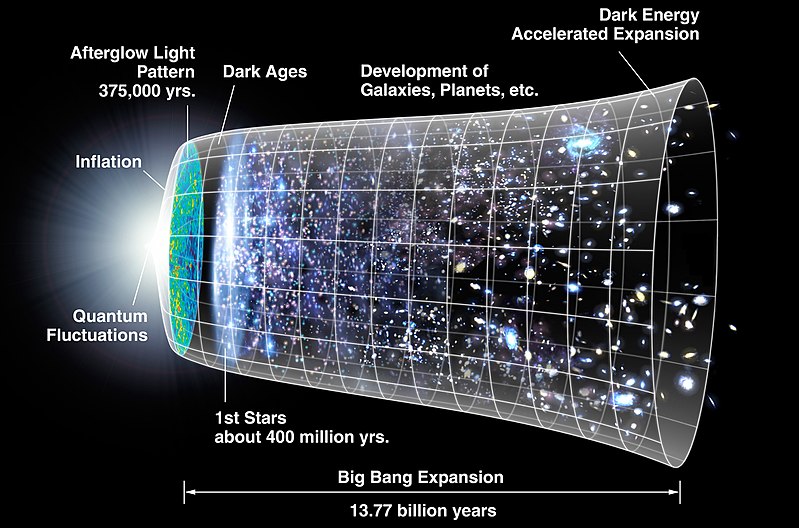
The very early universe was very dense and hot (T >>10⁴ K). The high temperatures meant that the baryonic component of the universe was completely ionized and opaque, producing blackbody radiation. In fact, it produced a huge amount of radiation: the baryon-to-photon ratio is estimated at 6 x 10^-10, meaning that there were 60 billion photons for each baryon. These photons were constantly bouncing off electrons like the proverbial energetic children bouncing off walls, although the collisions were becoming less and less frequent as the universe expanded (like kids coming down off a sugar high).  These blackbody photons are still present and detectable in the universe today; they are what we now call the Cosmic Microwave Background radiation (CMB).

As the universe continued to expand and cool, there are several key stages that we are concerned with. These include the epoch of recombination, the epoch of photon decoupling, and the epoch of last scattering. The epoch of recombination is the time at which the baryonic component of the universe (charged electrons and protons) went from being ionized to neutral as the electrons and protons became bound together–combined–to form atoms. Specifically, this is defined to be the moment that the number density of ions equals the number density of neutral atoms. (The term “recombination” should really be called “combination,” because it was the very first time electrons and protons became bound.) The epoch of photon decoupling is the time at which the universe began expanding faster than the rate at which photons scatter from electrons, causing the the interactions between the photons and electrons to end. This means the universe went from being “foggy” to transparent.

When the universe had sufficiently few electrons for the typical CMB photon to scatter off of one for the last time, the photons started streaming freely through space. We call this moment the epoch of last scattering, and the surface from which the CMB photons have been streaming since then is referred to as the surface of last scattering. The epochs of photon decoupling and last scattering are closely related, yet distinct events in the timeline of the early universe. Now, as these photons are streaming through expanding space, they are cooling off at a rate of T(t) ≈ a(t)^-1, where a(t) is the scale factor of the universe. Since the scale factor has increased by a factor of 1090 since the epoch of decoupling, the temperature of the CMB has dropped from about 2970 K to its currently measured value of 2.7255 K–a factor of 1090. For more information on the CMB, please visit this page for an excellent summary by my classmate, Alex.

Epoch	Physical Description
Recombination	The time at which the baryonic component of the universe went from being ionized to neutral as electrons and protons combined to form atoms.
Photon Decoupling	The time at which the universe began expanding faster than the rate at which photons scatter from electrons, causing the the interactions between the photons and electrons to end and the universe to become transparent.
Last Scattering	The time at which the typical CMB photon had scattered off of an electron for the last time; these photons have been streaming freely through space since then.

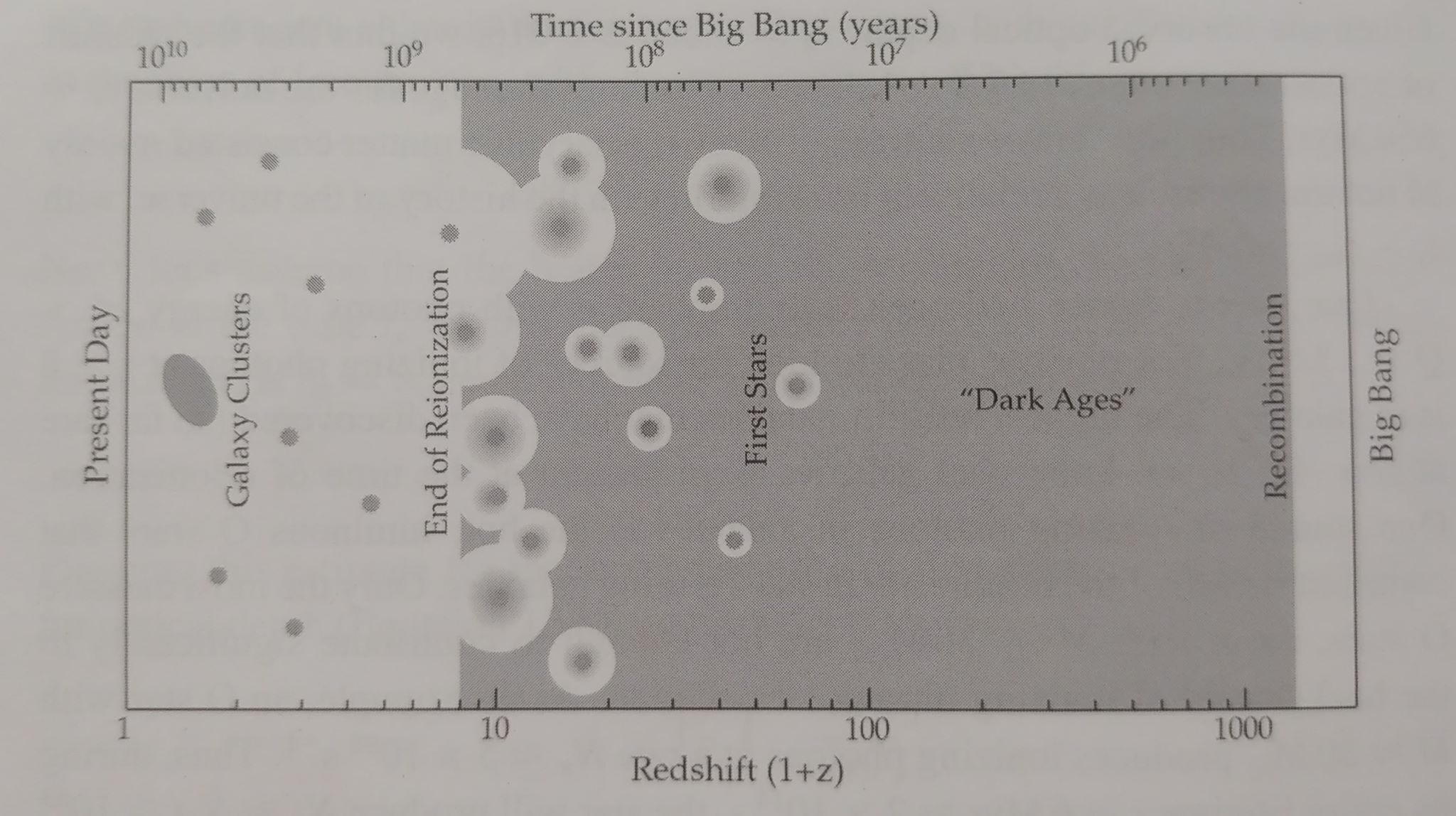
The Not-So-Dark Ages

Recombination occurred at roughly t ≈ 370,000 years after the Big Bang. The first stars are thought to have been formed between t ≈ 50-180 Myr after the Big Bang (yes, that is a bit of a range, but we’re doing the best we can; there isn’t a ton of direct observational evidence for us to go off of). The period between these two events is referred to as the “Dark Ages.” This term is another misnomer, though (who names these things, anyway?). Recall that the temperature of the CMB immediately after the time of last scattering was 2970 K–this is comparable to the surface temperature of a type M star, and therefore conveniently emitting wavelengths that are visible to us. If you could go back to this time without being instantly killed by the temperature, you would see the entire universe around you glowing like the surface of a star.

If, in addition to time-travelling capabilities and an incredibly temperature-resistant space suit, you were able to survive millions of years and decided to stick around in the early universe for awhile (maybe fast-forwarding through time?), you would notice the unrelenting expansion of the universe slowly dimming this glow (according to the receptors in your eyes, at any rate) as the CMB’s wavelength was stretched out from visible wavelengths to the far infrared. And during this process, the radiation would be becoming increasingly incapable of ionizing hydrogen. However, you wouldn’t be left in complete darkness for too long; the very first stars would begin flickering into existence at around the same time the CMB ceased to be ionizing radiation. They would continue forming at the rate of 20,000 M_☉Myr^-1 Mpc^-3, the same as the current star formation rate.

Gravitational Instabilities

We know that star’s aren’t distributed evenly throughout the universe; instead, they are clumped together. Viewed at large scales, they form a kind of cosmic web. How this happens will be our focus for the rest of this post.

To properly address the formation of structure, we need to go back to the very early universe. The CMB is not completely homogeneous; there are temperature fluctuations on the order of about 1 part in 100,000. This is a clue about the early universe–it tells us that the early universe had these small inconsistencies. It also means that once the radiation-dominated phase of the universe is over, denser regions will expand more slowly than the surrounding regions. This is actually good news for the formation of structure, because we can use physics describing gravitational instability to explain how galaxies formed. And given an inch, gravity will want to go a mile, with the small density fluctuations growing exponentially with time and the denser regions feeding on the less-dense regions to become larger and larger.

Now to get into the specifics. At the same time that a sphere of gas is compressed by its own gravity, it is also supported by the outward force of pressure. When the forces of gravity and pressure are balanced, we say that the sphere of gas is experiencing hydrostatic equilibrium. Now, if a region containing a density perturbation is to achieve hydrostatic equilibrium, there is an upper limit on its size, known as the Jeans length λ_J:

where where c_s is the local speed of sound, G is the gravitational constant, c is the speed of light, and  is the average energy density of the region.

Any perturbation region larger than the Jeans length is doomed to collapse under its own gravity, with its pressure utterly unable to keep up. The density of any region smaller than the Jeans length will simply oscillate in futility, in a war between its self-gravity and pressure, with neither one quite able to overcome the other.

The Jeans mass, M_J, is the mass contained within a sphere whose radius is the Jeans length (λ_J):

Photon decoupling turns out to be an important event in the timeline of density perturbations in the early universe. Until photon decoupling, the baryonic Jeans mass was too high for perturbations in baryonic density to grow in amplitude. However, during photon decoupling, the baryonic Jeans mass dropped from about 10¹⁹ M_☉to about 2 x 10⁵ M_☉. This huge drop in the Jeans mass instigated rapid growth in the density perturbations of the baryonic component of the universe.

Up until now, we have only discussed the perturbations in baryonic component of the universe. This isn’t the whole story, however. Our current model for the universe includes cold dark matter; in fact, dark matter, not baryonic matter, is the dominant form of nonrelativistic matter in the universe. This means that density perturbations in the universe actually started before photon decoupling. Perturbations in the density of the dark matter component of the universe began at around z = 3440, and then when photons, electrons and baryons decoupled at z = 1090, the baryons simply collapsed into the gravitational wells created by the dark matter.

Galaxy Formation

Now that we have some background on density perturbations in the early universe, we can move on to a simplified explanation for the formation of galaxies. Imagine we have a spherical region of the universe at the time the radiation-dominated epoch gave way to the matter-dominated one (t ∼ 0.050 Myr). We can relate the mass M of the sphere, its radius R, and its overdensity δ by

where is the average mass density of the universe at time t and redshift,

 Note that “overdensity” simply refers to the deviation of the density of that region of the universe from the average density of the universe.

The sphere will start collapsing under its own gravity when its overdensity δ ≈ 1. Since the time t_collapse at which the region will collapse is related to redshift through 1 + z_collapse ≈ δ_rm(1 + z_rm), where z_rm is the redshift at the matter-radiation equality and z_collapse is the redshift at the moment of the region’s collapse, we can say that the more overdense a region is, the sooner it will collapse (since a larger redshift means that it happened a greater length of time in the past).

Once it has collapsed, the spherical region of the universe will be a halo 8 times as dense as it was to begin with, and its average density is approximately

This comes in handy because it means that you can calculate when a galaxy’s halo began to collapse, based on its current average density. Another very handy relationship we can use here comes from the fact that the halo is in hydrostatic equilibrium (when the inward force of the halo’s self-gravity is balanced by the outward force of pressure). This allows us to use the relation between the temperature of the gas in the halo, its mass, and redshift:

where β is a value describing the gas profile, G is the gravitational constant, μ is the mean mass per gas particle, and ρ_m,0 is the mass density of the universe at the moment the sphere began collapsing.

Now, in order for a galaxy to form out of the halo created from the overdense region, the gas needs to be able to break out of the hydrostatic equilibrium. It can do this by losing energy from the emission of photons, therefore causing pressure to drop and the gas to fall inwards toward the center. The process by which ionized gas cools is called bremsstrahlung (say it in a German accent because it literally means “brake radiation” in German). In bremsstrahlung radiation, an electron emits a photon and loses kinetic energy every time it moves past a proton or ion–gotta love those accurately descriptive German words. The time it takes the gas to cool by bremsstrahlung emission is

where ε is the energy density of the gas, ψ is the luminosity density of the bremsstraulung emission, and T is the temperature of the gas. This equation essentially means that in order for the gas undergoing bremsstrahlung emission to cool within the age of the universe, it must have a density greater than 10^-24 kg m^-3.  And the average baryonic density of the halo is related to the redshift at which collapse occurs.

Basically, then, we have an interplay between the temperature and density of a halo, and the redshift at which it collapses. In order for a region to form a galaxy, it needs to be hot enough after collapse to be mostly ionized and undergo bremsstrahlung emission, and dense enough that it collapses early enough to cool within the lifetime of the universe. This is plausible for a halo with a mass of 10¹² M_☉ that began collapsing after the start of intense star-forming era (z > 4). It is not, however, likely to happen to a halo with a mass much larger than that.

This helps explain why observational evidence indicates a sort of mass limit in galaxies. This evidence is the observed luminosity function for galaxies: very few galaxies with luminosities greater than 20 x 10¹⁰ L_☉ exist, indicating that it’s very unlikely for a galaxy with a total mass greater than 10¹² M_☉ to exist. This lines up perfectly with the conditions for galaxy formation that we just discussed. It also means that galaxies that are larger than 10¹² M_☉ resulted from the merging of smaller galaxies.

Conclusion

This has been a very condensed and simplified summary of how galaxies formed in the early universe. In a nutshell, the web-like structure of filaments and walls that we see in the universe on large scales is a result of tiny fluctuations in the early universe that gave way to the runaway growth of density perturbations and eventually, gravitational collapse of overdense regions. We can explain the rarity of super-sized galaxies using fundamental physics based on the characteristics of the collapsing regions, and the time at which they collapse. And all of this can be done from the safety of your own office or home, without the need for time-travel or incredibly temperature-resistant space-suits. It’s amazing what a bit of physics can do!