By: Juan Manjarres, Kody Manstyrski, Kelsey Peppler, Mitch Dressler, Ricardo Rheeder
Introduction to the VW Hydrae System
VW Hydrae, first discovered by Cuno Hoffmeister in 1929 [1] within the Hydra constellation, is an Algol-type eclipsing binary system with an evolved secondary component. The system portrays a rapid period increase due to the possible presence of two additional, and yet, unseen components within the binary.
VW Hydrae is classified as an Algol-type binary system, which is a classification of eclipsing binary star systems. The Algol-type system is considered semi-detached because of its main sequence star that does not fill its Roche Lobe. The Roche Lobe is an area around a star in the binary system which uses gravitational forces to bind the orbiting material to the main component. If it expands past this lobe, the material will fall onto the secondary component [2].
To analyze the aforementioned effects that the binary system has been experiencing, the primary component’s apparent and absolute magnitudes will be recorded and used within equations to acquire the temperature and period of the system. The ‘apparent magnitude’, denoted as ‘m’, is a common measurement used to reference an astronomical object’s brightness as seen from Earth, whereas the ‘absolute magnitude’, denoted as ‘M’, is used to describe the intrinsic brightness of the object if it were 10 parsecs from Earth. The lower the absolute magnitude, the brighter the object appears to be, with the Sun having an apparent magnitude of -26.74, the moon having an apparent magnitude of -12.7, and Venus having an apparent magnitude of -4.89, for example.
Any object with an apparent magnitude greater than +6 is too dim for the human eye to perceive and is thus a good baseline to consider when wanting to determine if a star is visible in the night sky. VW Hydrae prossesses a maximum apparent magnitude of 14.1 and a minimum apparent magnitude of 10.5, meaning that VW Hydrae is not visible to the naked eye throughout the night.
The various lens filters used in astronomy prevent the light of specific sections of the total light spectrum from reaching the camera or observer, and the image that is created is the result of intensities (the strength or amount of) light in the non-filtered spectrum reaching the camera. The colours relevant to the temperature calculation are the B, for blue, and V, for visible, filters. The value of B-V is merely the difference between the magnitude (intensity) of light gathered from the observations using the respective filters. This value provides the key value for obtaining temperature using the formula.
Components within the system
Following Hoffmeister’s observations, Kviz & Rufener published photoelectric observations in UBV bands in 1987. The observations showed that there is a secondary component, which is too deep in the U-band and provided evidence that there is an ultraviolet source in the system that must be eclipsed during the secondary eclipse – when the secondary component is visibly blocked by the primary component [3]. In 2005, Burki published the first radial velocity curves for both components and the complete light curves in multiple bands [1]. Burki classified the spectral types of both components as B8/9V for the primary component and F9III for the secondary component.
This paper will consider four components within the system which will be denoted as Source1, Source2, Source3, Source4, with Source1 referring to the primary component within the binary system and Source2 referring to the secondary component. Source3 and Source4 refer to the two additional components found within the system and are the components potentially affecting the system’s elliptical period and the temperatures of both Source1 and Source2.
It is suspected that the ultraviolet source may be one of the additional bodies. Furthermore, because of the masses of the Sources, Source3 and Source4 could possibly be main-sequence stars, unseen neutron stars, or black holes. If a Source was a main-sequence star, it should have been very luminous and easily detectable during observations. However, since no signal of the additional components was reported by Burki et al. (2005) from their photometric and spectroscopic observations, it is possible that either Source could be an unseen neutron star or black hole.
Previous efforts to generate measurements
Previously, efforts have been made to generate the accurate measurements of these components, with the most credible being due to the efforts of using Geneva seven-colour photometric measurements [4] and photometry obtained with the Wilson-Devinney WD program with a revision produced in 1995 [1]. The Geneva seven-colour photometric measurements of VW Hydrae were obtained from 1983 to 1990, where the magnitudes in each of the seven filters are obtained from the visual magnitude V and the six colour indices (U, B, B1, B2, V1, G). The Wilson-Devinney WD program allowed for a simultaneous computation on the light curves and the radial velocity curves of both components, ultimately contributing to the calculation of the various variables tabled: [4, table 6].
Previous measurements of the temperature obtained
The Geneva measurements were able to determine the effective temperature measurements using obtained color indices of the primary component: i = V [V-B] + [i-B], where i represents one of the seven filters. The temperature would then be calculated using these color indices and some additional calculations with the flux. These values would then be used with the Wilson-Devinney program to get more certain results. The estimated temperature of Source1 would then be [B2 – V1]0 = T1 = 10.650 ± 200 K according to the photometric calibrations. For Source2 the photometric evaluation of the temperature would be very imprecise due to the large uncertainty on [B2 – V1](0.65 ± 0.28), hence, the best value was calculated as T2 = 4848 ± 7 K.
Previous measurements of the period obtained
The period, P, of the binary system is measured in relation with Source1, Source2 and their center of mass. The orbital period was recorded as P = 2.696423 days in 1985, and was later recorded as P = 2.6964378 days by Kviz and Rufener in 1987 [4, Table 5]. The period increase may be caused by a combination of the mass transfer from the secondary to the primary and the angular momentum transfer from the binary system to the circumbinary disk. It was calculated that the linear period increase is 4.1 ms per period [4].
Previous measurements of masses obtained
Each Source possesses a mass and is mapped respectively: M1, M2, M3, and M4. The masses are measured in units of solar masses, M⊙, i.e. multipliers on the mass of the Sun. Using the photometric solution and obtaining a fixed temperature for Source1 as T1 = 10,650 K, M1 is computed to be 3.10 ± 0.07 M⊙ and M2 is computed to be 0.76 ± 0.02 M⊙.
The small amplitude periodic change indicates the existence of a less massive component with mass M3 > 0.53 M⊙, while the large-amplitude one is caused by the presence of a more massive component with mass M4 > 2.84M⊙ [1]. M3 and M4, having a massive mass, yet no observable magnitude indicates the presence of an unseen neutron star or black hole.
Common Methodology
Gathering images and data
In recent times, common methodology includes retrieving images from observations of the desired system by using a tool, such as Skynet, to schedule observations over the course of the desired time period. After aligning the images in their respective filters, multi-aperture photometry in the system is performed; this is where a light curve and the measurements of the flux values are obtained. The light curve and obtained measurements would then be used further to calculate different variables of the system in question.
Period
Commonly, the semimajor axis (a) in Astronomical Units, “AU”, is required to retrieve the period of a system. The semimajor axis is one half of the major axis of the ellipse that one celestial body describes around another. If the semimajor axis is known, there is a direct relation between the system’s period (in years) squared and the semimajor axis (in AU) cubed. Furthermore, with sufficient amounts of observations, one can examine the dips in the light curves to get an estimation of the period.
Temperature
A common methodology to retrieve the surface temperature of individual stars (that exist on the main sequence) within a binary system is to retrieve the star’s luminosity using the Mass vs. Luminosity relation. Using the luminosity, the temperature can then be retrieved through the Luminosity vs. Surface Temperature graph, however, the results will often not be accurate enough, due to estimates taken when plotting the values onto the graphs. Thus, there are other methods involving the luminosity, radius, and temperature relationship as well as using the flux vs. Julian date values obtained through observations, to insert into a tool named “Binary Maker 3” to retrieve the temperatures of the primary and secondary components within a binary system.
Equations and definitions
1. Ballesteros’ formula: Necessary for calculating the temperature of the system using the B-V index.
T: The temperature of the system
B: The magnitude of the system in the Blue spectrum
V: The magnitude of the system in the Visible spectrum
2. Phase Value formula: Necessary for converting Julian date values to phase values [5]
Phase: Where the star is within it’s cycle
HJD: Julian Date Values
T0: Earliest Julian Date Value in the series
P: The period of the system
INT: The floor function; to convert to a value between 0 and 1
3. Magnitude formula
mA: The magnitude of Star A (VW Hya)
mB: The magnitude of the Star B or reference star
fA: The flux value of Star A
fB: The flux value of Star B or reference star
4. Main Sequence Life Expectancy
t: The main sequence life expectancy of the star in question.
t⊙: The main sequence life expectancy of the Sun.
M: the mass of the star in question.
M⊙: The mass of the sun.
Expectations
This paper will aim to present noticeable changes in the period and/or temperature that the system, or it’s components, have undergone. The procedures and results that follow will be well documented to allow for reproducibility and/or improvement. Furthermore, there will be a discussion on the future changes the system may experience, as well as where it currently may be standing on the H-R diagram and its remaining lifespan.
Methods and Data
The intention of this research is to target the VW Hydrae system and obtain photometric observations using telescopes R-COP and PROMPT with U, B, R, and V filters. Given that the period of VW Hydrae is reportedly approximately 2.7 days, multiple observations were taken every 24 hours to obtain data, but as the obtained observations were not enough to complete the light curve for the system, more observations were taken at least every 30 minutes to cover the full cycle of the system.
Period
Over the span of 9 days, a total of 360 images were gathered, and of that, about 10% of the images were faulty due to “WCS registration failed” errors provided by Skynet. After discarding the faulty images, and plate solving the images without WCS coordinates, the images were aligned three times using AstroImageJ – which did not provide the expected results and failed to provide consistently aligned images, thus the results were aligned an additional time using Maxim which successfully provided consistently aligned images.
Because the gathered data was not sufficient to create a reliable light curve, 50 more observations every 30 minutes over the span of 7 days were taken. These observations were made in both B and V filters, to gather more data about the temperature of the system.
The aligned images were used in conjunction with AstroImageJ to produce a Flux vs. Julian Date graph and an excel file. The flux values were then converted to magnitude using equation 3, in which the reference star is 111, as per Figure 6.
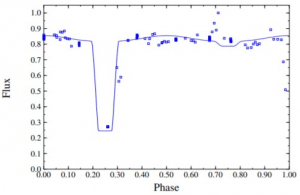
Based on the magnitude vs. Julian Date values, a different csv file was created, containing just these two parameters. Then, the csv was opened using Period Search, in which the minima of the Jurkovich method represents the approximate period of the system.
The Julian Date values from the excel file of AstroImageJ were converted to phase values using the Phase Value formula (equation 2) with the period gathered from Period Search. These values only contained the data from the V filter. Then, a new excel file was created, containing only the phase values in one column, and the flux values in another column. This excel file was saved as a .txt file, which was later modified to .mag for reasons of compatibility with Binary Maker 3.
Individual star’s temperatures
For the VW Hydrae binary system, where both Hya A, Source1, and Hya B, Source2, exist on the main sequence, the methodology to gain an estimate of each star’s individual temperature is to retrieve the star’s luminosity, and retrieve the surface temperature of that star using the Luminosity vs. Surface temperature relation graph.
If the estimated value described above proves to not be sufficient enough, more accurate data will be retrieved with the use of Binary Maker 3.
In Binary Maker 3, the .mag obtained in 2.1 was opened by clicking the File Menu in the Light Curve Plot window and selecting “Open phase/magnitude file…”. There, a few parameters were adjusted: the Omegas in the User Input tab were modified to Omega 1 = 12.0 and Omega 2 = 2.35, to reflect the nature of the semi-detached binary system, and the mass ratio was set to 0.245, as per the mass values obtained by Zhang [1].
System Temperature
The methodology for obtaining the temperature was two-fold. Obtain csv of photometric data, and separate and obtain index differences and apply the above index-temperature formula. The values for the indices are obtained through the use of filters on a CCD camera.
The software which gathers the images, known as Skynet, and processes the imagery data, known as afterglow, also provides a handy service by giving the magnitude of the ‘object’ of the image (only one ‘object’ per image). This value is what the specific colour index refers to. The CSV (comma-separated values) file, from which the magnitudes of the B and V values were obtained, was itself obtained from this software system using the included photometry tool.
The above CSV then was manipulated to remove superfluous data points, and to line up the relevant data points side by side. Two additional columns were then added to the data, and the calculated values of B – V were placed in the first of the new columns. The second new column was filled with the temperature values calculated using the formula 1. Finally, an additional row was added below the rest, and the average of each column of data was placed here.
Main Sequence Plotting
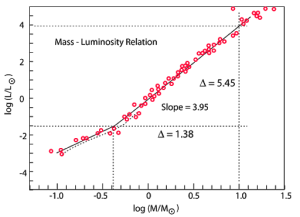
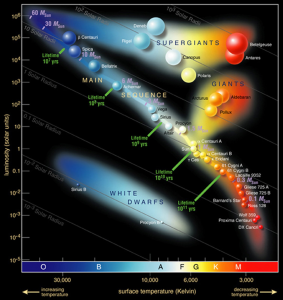
Using the mass values from the introduction (1.3.3), and the below mass vs. luminosity relationship graph (Figure 7) for the relationship between mass and luminosity, the values for the luminosities of Sources1 and Source2 were obtained. An HR diagram (Figure 8) was then consulted to roughly determine the types of the stars, and determine main sequence eligibility, and thus fitness of Equation 1.5.4. This equation was then used in conjunction with the obtained luminosities to determine the lifetime expectancy of the respective stars.
Analysis and results
Period
Following the methodology outlined in 2.1, the .csv file with the Julian Date values and the magnitudes was opened in Period Search, where a minima represents a very probable period for the system. Because of the known values of around 2.69 days, the curve was zoomed in a range of about 0.1 days, as shown in Fig. 2. In this zoomed in range, the light curve with the best plot had a period of 2.68 days. Therefore, this period was used throughout the calculations for Binary Maker 3, and is assumed to be the new period of the system.
Figure 1: Period Search image of Jurkovich method from 0.2 to 3 days.
Figure 2: Period Search zoomed in from 2.65 days to 2.73 days.
Individual star’s temperatures
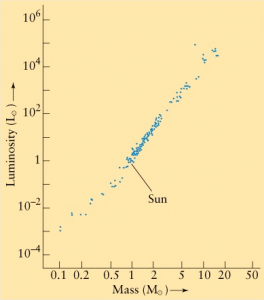
Following the methodology to retrieve the estimated temperature of Source1 and Source2, the star’s luminosity was gained through the Mass vs. Luminosity relation, Figure 3. Thus, with Source1 having a mass of M1 = 3.10 ± 0.07 M⊙, using Figure 3, Source1 gave the corresponding luminosity of approximately L1 = 102L⊙. With Source2 having a mass of M2 = 0.76 ± 0.02 M⊙, using Figure 3, Source2 would have a corresponding luminosity of approximately L2 = 7×10-1L⊙.
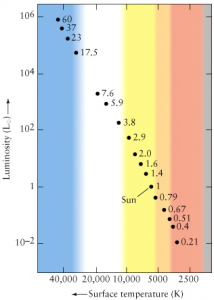
Using the aforementioned estimated luminosity values, the surface temperature for each star was obtained using the Luminosity vs. Surface Temperature relation, Figure 4. With Source1 having a luminosity of L1 = 102L⊙, using Figure 4, Source1 was found to have a corresponding surface temperature of approximately T1 <= 10,000K. With Source2 having a luminosity of L2 = 7×10-1L⊙, using Figure 4, Source2 would have a corresponding surface temperature of approximately T2 <= 5,000K.
With the previously published temperature values of T1 = 10.650 ± 200K and T2 = 4848 ± 7K, these rough estimates proved to not be useful for the analysis our hypothesis requires. Following this predicted outcome, the methodology described in Section 2.2 was continued.
Following the methods in Section 2.2 for Binary Maker, the file was opened and the parameters were set as stated. To obtain the temperature values, the already known values were input into the system to contrast with the light curve generated beforehand. After changing the values a few times, and matching the light curve as much as possible, it was seen that the temperature of the system remains stable, as Source1 registered a temperature of 10550K, and Source2 registered 4848K.
Figure 5: AAVSO Star Chart for VW Hya
Figure 6: Photometry chart of reference star TYC 5441-1062-1
System Temperature
With 125 observations, the values relevant to the temperature calculations were placed in Table 1. These values were obtained by applying the relevant calculation or statistical operation on the observed magnitudes. For example, the system temperature average was obtained through calculating the temperatures of each B-V value, and then taking the average of the results. The system temperatures themselves were found by equation 4.
| Average M | Standard Deviation | |
| B | -9.067432793 | 1.05 |
| V | -9.55341279 | 0.97 |
| B-V | 0.485979997 | 0.22 |
| System Temperature (Kelvin) | 6602.113322 | 912.10 |
Table 1: Averages and Standard Deviations in the Observed Blue and Visible Indices and System Temperature.
Main Sequence Plotting
Luminosities from masses
Figure 7 was referenced to obtain the relationship between the masses and luminosities. As mentioned in Section 1.3.3, the masses of Source1 and Source2 respectively are 3.1M⊙ and 0.76M⊙. The values obtained from applying the base 10 logarithm on these values are 0.49136169383 and -0.11918640771 which gives the location on the x-axis of the graph that the luminosity corresponds to. Referencing the y-axis of the same graph then roughly gives the logarithm of the star’s solar luminosity (log(L1/Lsun) ~= 2, log(L2/Lsun) ~= -2.1). Raising 10 to this value then results in the luminosity in solar luminosity (L1 = 102L⊙, L2 = 10-2.1L⊙).
Plotting on an HR Diagram
Given the temperatures from the in Section 1.3.1 and referencing the H-R diagram (Figure 8) it was found that the stars are main sequence stars, with Source1 being blue and Source2 being orange.
Calculation of Life Expectancy
With the luminosities and previous temperatures in hand, equation 4 was then used with a value for t⊙ as 1.2*1010 years and mass ratios of M⊙/M1 = 0.323, and M⊙/M2 = 1.32 to obtain the life expectancies of Source1 as t1 = 5.93*108 years and Source2 as t2 = 2.00*1010 years.
Discussion
HR Diagram Result Analysis
As noted above, Source1 and Source2 are main sequence stars of blue and orange types respectively with a rough life expectancy of around t1 = 2.03*1011 years and t2 = 6.04*109 years. A significant change in temperature would contradict this information, since then one or both of the stars would be advancing through its/their life cycle faster than expected. This would then imply some sort of interference in the normal cycle of a star. This interference could be because of mass transfer between binary components, or because of some third actor in the system.
In the former case it would imply a change in radii in both of the components, while the latter would imply a change in period, and a change in the radius of only one of the components. In the case of both a change in radius and a change in period with any significance, the matter is more complicated. A third element could explain a lengthening of the period or a change in mass, but not both. If a third component is close enough to transfer masses from both, it cannot lengthen their period, and if it lengthens the period then it must be far enough to avoid mass transfer.
Key Results
The significant values obtained from the experiment includes the system’s period of 2.68 days, Source1’s temperature of 10,550 K, and Source2’s temperature of 4,848 K. This, in comparison with previously published values (the system’s period of 2.6964378 days, Source1’s temperature of 10,650K, and Source2’s temperature of 4,848 K [4]) demonstrates the possibility that there has been no noticeable effect on the system due to the additional Sources present in the system.
Due to the difference of 0.0164378 days between the two values for the system’s period, there seems to be a decrease of the period; becoming a resulting factor from the binary system contracting due to the gravitational effects of additional Sources (or due to natural evolution of the stars), however, this difference is far too small to hold any viable significance. Furthermore, for the individual temperature of both Sources; the new value found for Source1’s temperature 10,550 K lies in the bottom half of the previously published value of 10,650 ± 200 K, whereas Source2’s temperature has no distinct change compared to its published value. Although very insignificant in value, there exists small hints of a decrease that may also be a result of the effect the additional components may have had on the system. Due to the period decreasing slightly, and an assumption of the binary system contracting, we can assume that these effects have contributed to the cooling of the stars, along with each star’s expected evolution process.
Interesting Findings
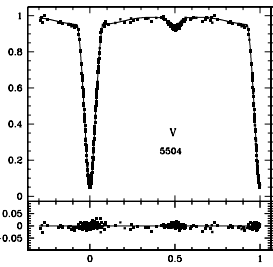
Once the light curve was generated (as shown in Figure 9), it displayed a strong resemblance to the previously published light curve demonstrated in Figure 10. The phase displays the duration of one complete period, demonstrating the different flux values the system undergoes throughout its cycle. Both light curves display the two minimas, however Figure 9 displays additional abnormalities, with peaks detaching from the expected curve, that could possibly be due to the additional Sources in the system. However, with insufficient amounts of data, it is difficult to base any conclusions off of this assumption. Due to observation errors in the images gathered from the ultraviolet spectrum, the deep U-band is unable to be analysed, thus no conclusions could be made on the deep U-band during the secondary eclipse.
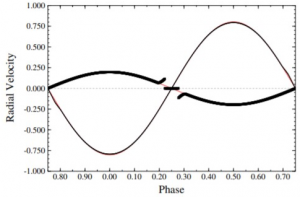
As mentioned throughout the paper, Source1 is classified as a blue star with a mass of M1 = 3.10 ± 0.07 M⊙ and Source2 classified as an orange star with a mass of M2 = 0.76 ± 0.02 M⊙. With this in mind, following Figure 10, Source1 is the thicker curve reaching a lower peak as it is the heavier star, whereas Source2 is the thinner curve reaching a peak in radial velocity which is three times greater than that of Source1.
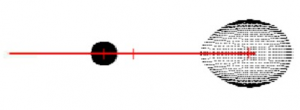
Additionally, Source1 would be smaller and more dense than Source2, possessing the characteristics of a Semi-detached Binary System. Source2, being the orange star, seems to have filled its Roche lobe, possibly spilling mass to Source1. In time, the system may develop to a Contact Binary System in which material would flow from one star to the other across the inner Lagrangian point. When both stars have overfilled their Rosche lobes, the stars will share a common envelope of gas, forming an Overcontact Binary. As an Algol Binary System, it is an expected behavior that the system is a Semi-Detached Binary.
Challenges encountered consisted of the following:
- Learning AstroImageJ: AstroImageJ has many features and options that in the beginning are somewhat confusing. The manual certainly did help, but a lot of it comes down to trial and error. The alignment of the images was a huge challenge as multiple times the images came out misaligned or with missing coordinates. Through plate solving the images using astrometry.net, as well as using MaxIm DL6 to align some of the images helped to overcome the challenges.
- Creating a folded light curve: AstroImageJ served as a reference here but Microsoft Excel was very useful to create light curves that could change in reference to the input period.
- Learning Binary Maker 3: Binary Maker 3 is also as feature-packed as AstroImageJ. However, Binary Maker 3 has a much in-depth guide about the different input values and windows, and it has a few models to understand it. It took a long time to understand the different parameters and how the system worked with the file types, but at the end it was possible.
Sources of Error
A major source of error may be the number of observations made – at least 50-100 observations should be made whereas we obtained 360 observations taken in a group of 9 clusters across 9 days, i.e. observations were scheduled every 24 hours as opposed to every 30 minutes. Furthermore had to discard roughly 18 images due to errors in the data. After the initial flaws were noticed, and due to time constraints, another 50 images were scheduled for every 30 minutes across 7 days where an additional 6 images had to be discarded. With an inconsistent amount of images across timespans, the generated light curve would have had enough data to produce the necessary minimas to make observation precise.
Error in the life expectancy calculation was mostly from the resolution of the axes on the graphs referenced. The axes on Figure 7 step by one tenth along the x-axis and one on the y-axis. This meant that some level of rounding was required to find the location for the relevant values, as well as some degree of uncertainty in selecting the ‘exact’ location. The HR diagram (Figure 8) had similar issues with the temperature value (x-axis) being in logarithmically scaled steps, and the luminosity being in exponentially scaled steps. Similarly with Figure 7 some amount of uncertainty in picking where the temperature values and luminosity values fall ‘exactly’. In both cases a close enough location was used, which introduced uncertainty. Finally, inherent uncertainty in the observations used will propagate further with the work, especially when coupled with the issues mentioned before. The uncertainty from the observations themselves is currently unavoidable since it is inherent in the raw data gathering methodology. The uncertainty from the mass vs. luminosity relationship could be avoided completely if a precise equation were to be used, or if a graph with more fine grained units along both axes were to be located.
Conclusions
Key findings
As a result of the experiment and careful calculations, the newly calculated value of the temperature for Source1, Hya A, of TS1New = 10,550 K is within the lower spectrum of the previously calculated value of TS1Old = 10,650 ± 200 K. This comparison demonstrates a small loss of temperature and could, therefore, be affected by the existence of the additional components, Source3 and Source4.
The newly calculated value of the temperature for Source2, Hya B, of TS2New = 4848 K is equivalent to the previously calculated value of TS2Old = 4848 ± 7K . This comparison demonstrates a maintenance of temperature and is not therefore affected by the existence of the additional components, Source3 and Source4.
The newly calculated value for the system’s period, P = 2.68 days, as compared to the previously published period of P = 2.6964378 days demonstrates that the system is indeed possibly experiencing a slow contraction, which may be an effect of the additional components within the system.
Significance of results
These comparisons demonstrate that the additional Sources may be impacting the speed/distance of the Hya System. Because Source3 and Source4 are too small to be observed and their masses are considerably high – with visibility in the U filter, either could possibly be a Black Hole or Neutron Star. Thus, these additional component’s high gravitational pull may have a small effect on Source1 and Source2.
Furthermore both Source1 and Source2 are Main Sequence stars with a lifetime of t1 = 5.93*108 years and t2 = 2.00*1010 years respectively. This demonstrates that the system will most probably experience the following effects within its lifetime: material transfer, eventual white dwarf evolution of Source2 after a period of being a Red Giant, a nova (the luminous mass transfer causing an accretion disk around a white dwarf companion) with Source2 at its center when Source1 becomes a Giant, and eventually a supernova. Based on the period, and the masses of these stars it is likely that a type Ia supernova, which is the explosive result of nuclear fusion of hydrogen in the atmosphere of a white dwarf in a close binary system, will occur.
Lessons learned
As a novice research team learning and gathering data, our team should have maintained open communication with individuals who possess more experienced knowledge on the procedures we aimed to follow and the results we had gathered. Thus, there would be minimum uncertainties throughout the research.
With the system experiencing a period of roughly 2.7 days, the research would have greatly benefited from more data points taken approximately every 30 minutes over the span of a few weeks. Because of a few human errors, the data points gathered for the research were gathered over the span of a few days as opposed to a few weeks/months, which may contribute to providing inaccurate results. As a result, precise minimas could not be obtained, hence an estimate for the period from Period Searcher was used throughout the analysis and could be inaccurate to a certain degree.
While using AstroImageJ and Binary Maker 3, it was very useful to create Excel files for the different filters used, as well as keeping track of the different files used in Binary Maker and Period Search, since it was necessary when testing for different periods of the system. User guides also turned to give a rough idea of both Binary Maker 3 and AstroImageJ, but trial and error helped through steps where there was not much guidance.
Throughout, the research team have gained insight into scheduling observations using Skynet, aligning images using AstroImageJ, creating folded light curves, and using Binary Maker 3 to further analyze the data of the curves. Furthermore, the team has learned various ways of publishing the results and formats to follow throughout.
Future work
The future work for the analysis of the VW Hydra system would include reproducing the procedure outlined in the G. Burki, F. Barlan, F.Carrier paper [4]. Following a reproduction involving the GENEVA seven-colour light curves, the results could more accurately be compared to previously gathered results, thus creating more correct conclusions of the effects of the additional components within the system.
Furthermore, the gravitational effects on the stars could be gathered by acquiring the radial velocities and creating a comparison between current velocities and previously gathered data to examine if there has been any increase or decrease in the speed of either the Hya A or Hya B. This could further model more estimations on the evolution and effects the VW Hydra system will be experiencing in the distant future.
References
[1]: Jia Zhang, Sheng-Bang Qian, and Boonrucksar Soonthornthum. An orbital period investigation of the Algol-type eclipsing binary VW Hydrae. May 8, 2008. Accessed July 4, 2008
[2]: Algol Wikipedia https://en.wikipedia.org/wiki/Algol_variable
[3]: Color Index Wikipedia
[4]: Physical parameters of the Algol system VW Hydrae from simultaneous analysis of GENEVA seven-colour light curves, by Burki, Barblan and Carrier
[5]: Variable Stars and Phase Diagrams:
- https://www.aavso.org/sites/default/files/Chapter12.pdf
- https://astronomy.stackexchange.com/questions/17863/deriving-phase-of-a-pulsating-star-from-list-of-julian-date-values-of-observing
[6]: Period Search by Bob Nelson: https://www.variablestarssouth.org/software-by-bob-nelson/